|
|||||
|
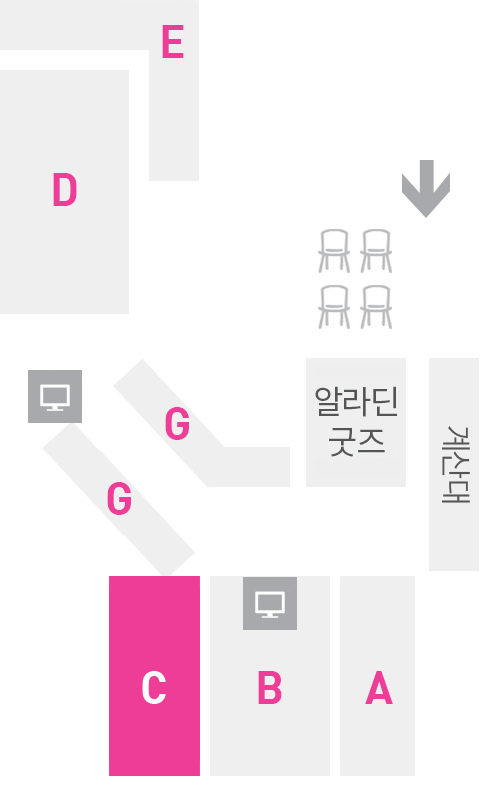
[종로점] 서가 단면도
|
|
|||||||||||||||||||||||||||||||||
|
|||||
|
[종로점] 서가 단면도

|
|
|||||||||||||||||||||||||||||||||